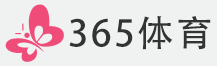对于三角形ABC，B = 600，AC =，AB + 2BC的最大值为（

测试点名称：求解三角形解的三角形定义。
通常，三角形的三个角A，B，C及其相对的边a，b，c被称为三角形元素。
查找三角形的某些元素并查找其他元素的过程称为三角形解决方案。
主要方法：
正弦定理和余弦定理。
解决三角形的一般方法：
1）
已知三角形将在一侧和两个角上分解：已知的一侧和两个角（设置为b，A，B）以及解析三角形的步骤：2。
对角线解的三角形的两侧和一侧：已知三角形的两侧和一侧的对角线。找到三角形的其他角时，首先需要确定是否存在解。例如，已知在此过程中没有解决问题的方法。
如果有解决方案，那就是解决方案或解决方案。
下表中显示了解决方案的数量。
已知双方及其角度可求解三角形：已知双方及其角度（在a，b，C中设置）以及求解三角形的步骤：4。
三边解三角形是已知的：三边a，b和C是已知的解三角形的步骤：使用1余弦定理求出角度。用正弦定理2和A + B + C =π查找其他两个角度。5）
确定三角形的形状：要确定三角形的形状，必须考虑三角形的角之间的关系，主要是确定它是等边三角形，等腰三角形，直角三角形，钝角三角形还是三角形。如果您很敏感，请特别注意“等腰三角形”。等腰三角形或直角三角形之间的差异由已知条件下的角度关系确定。有两种主要方法。1使用正定和余弦定理通过分解，表达式等将已知条件转换为边关系。获取边缘的对应关系并确定三角形的形状。2使用正定理和余弦定理将已知条件转换为内角三角函数之间的关系，并通过三角常数转换获得内角关系。因此，确定格式。应当注意，在三角形的这个时间，A + B + C =π成立。通常，在对前两个解方程进行转换时，这两个方面不需要求公因数，必须使用变化因数来提取公因数。
应用对角三角形的总体思路如下。（1）准确理解问题的含义，从所寻求的内容中区分出已知信息，准确理解应用程序的名称和相关术语（坡度，高程，下陷等），视角，象限角度，方位角，转向角等（2）根据问题的意思画图。（3）将求解问题附加到一个或多个三角形上，使用相关知识（例如正弦或余弦定理）建立数学模型，然后正确求解。计算过程简洁，准确，最后得到了答案。流程图可表示如下：在使用正弦和余弦定理求解三角形积分问题时，请注意三角形的三个内角的三角函数。
以上内容是Magic Square的学习社区（www。
Mofunge
Com）未经许可不得播放原始内容！